[알고리즘] 이진탐색
이진탐색이란?
- 정렬된 배열에서 특정 값을 찾는 알고리즘
- 이진탐색은 탐색 범위를 절반씩 줄여나가기 때문에 선형탐색에 비해 빠른 속도를 보장합니다. 하지만 배열이 정렬되어 있어야 한다는 조건이 필요하기 때문에 배열이 정렬되어 있지 않은 경우에는 정렬 작업이 필요합니다.
선형탐색이란?
- 배열(Array)이나 리스트(List)와 같은 데이터 구조에서 특정한 값을 찾는 알고리즘 중 하나입니다.
이진탐색 과정
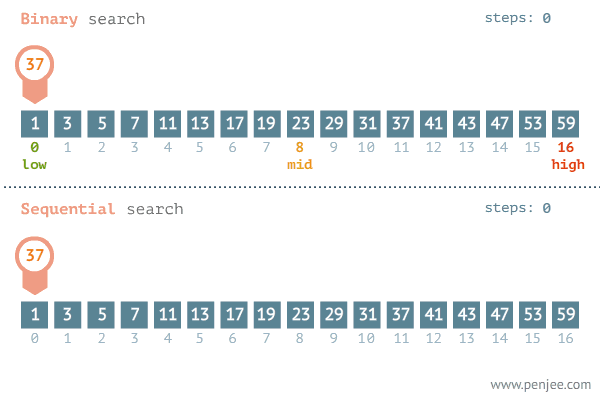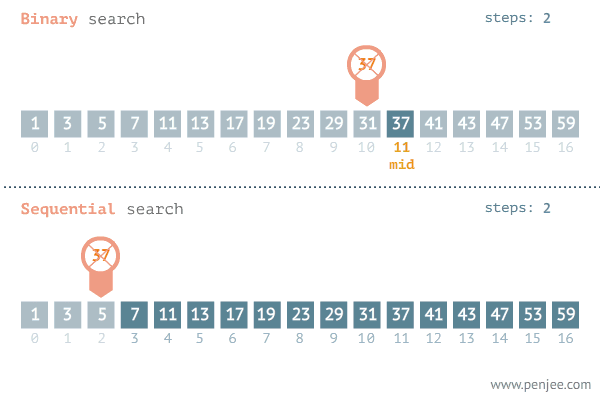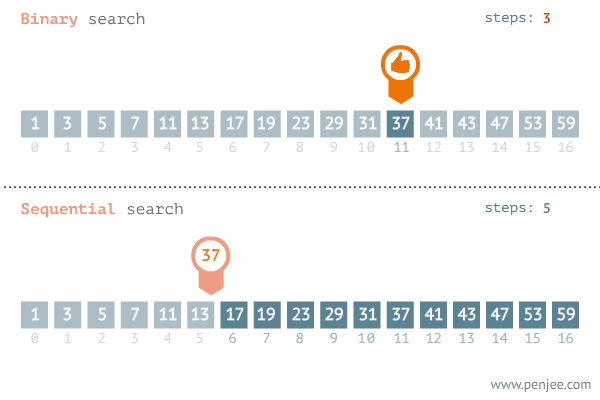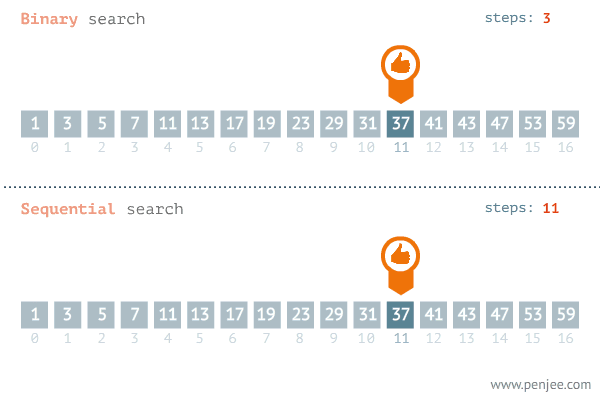
| 1. 배열의 중간 값을 선택하여 찾고자 하는 값과 비교합니다. 2. 만약 중간 값이 찾고자 하는 값보다 크면 '배열 왼쪽 부분'에서 탐색을 진행하고, 값보다 작으면 '배열 오른쪽 부분'에서 탐색을 진행합니다. 3. 이 과정에서 찾고자 하는 값이 나올 때까지 반복합니다. |
이진 탐색과 for문(선형 탐색)의 차이점이 뭘까요?
- 일반적으로 이진 탐색을 이용하여 값을 찾는 방법이 for문을 이용하는 것보다 빠릅니다.
- 이진 탐색은 정렬된 배열에서 원하는 값을 찾는 알고리즘이며, 중간값을 찾아 탐색 범위를 반으로 줄이면서 값을 찾아갑니다.
- 이에 비해 for문은 배열 전체를 순회하면서 값을 찾기 때문에 배열의 크기와 상관없이 속도가 일정하게 증가합니다.
이진 탐색은 언제 쓰면 좋을까요?
- 이진 탐색은 데이터가 오름차순으로 정렬되어 있을 때 특정한 값을 찾아야 할 때 사용합니다.
- 데이터의 양이 많을 경우에도 빠른 시간 내에 값을 찾을 수 있어 많이 활용되고 있습니다.
이진 탐색의 성능
- 이진탐색의 경우 시간 복잡도의 '빅오 표기법'을 이용하여 확인하였을 때 로그 시간인 O(log N)으로써 다른 정렬에 비해 상대적으로 매우 빠릅니다.

| 표기법 | 이름 | 시간 복잡도 | 설명 | 예시 |
| O(1) | 상수 | 상수 시간 | 입력 크기와 상관없이 일정한 실행 시간을 가집니다. | 배열에서 원소 하나 찾기 |
| O(logn) | 로그 | 로그 시간 | 입력 크기가 증가함에 따라 실행 시간이 로그함수의 형태로 증가합니다. | 이진 탐색 알고리즘 |
| O(n) | 선형 | 선형 시간 | 입력 크기와 비례하는 실행 시간을 가집니다. | 선형 탐색 알고리즘 |
| O(nlogn) | 로그 선형 | 선형 로그 시간 | 입력 크기가 증가함에 따라 실행 시간이 로그함수와 선형 함수의 곱의 형태로 증가합니다. | 병합 정렬, 힙 정렬 알고리즘 |
| O(n^2) | 이차 | 이차 시간 | 입력 크기의 제곱에 비례하는 실행 시간을 가집니다. | 선택 정렬, 버블 정렬, 퀵 정렬 알고리즘 |
| O(2^n) | 지수 | 지수 시간 | 입력 크기의 지수에 비례하는 실행 시간을 가집니다. | 부분집합 |
| O(n!) | 계승 | 팩토리얼 시간 | 입력 크기의 팩토리얼에 비례하는 실행 시간을 가집니다. | 외판원 문제 |
| 알고리즘 명 | 최악 시간 복잡도 |
| 이진 탐색 | O(log n) |
| 보간 탐색 | O(log(log n)) |
| 해시 탐색 | O(1) |
| 선형 탐색 | O(n) |
| 깊이 우선 탐색 | O(V + E) |
분할 정복
탐색 공간을 특정 기준에 따라 나누고, 나눈 각 탐색 공간에서 탐색을 이어 나가는 것을 분할 정복이라고 합니다.
binarySearch() 메서드 직접 구현하기
1. 범위 찾기
- arr의 인덱스를 찾는 과정으로 arr의 인덱스 범위인 0~arr.length - 1이 탐색 범위가 됩니다. 이는 [0, arr. length)처럼 표기할 수 있습니다.
- 찾은 범위는 다음과 같이 각각의 변수로 선언합니다.
int start = 0; // inclusive
int end = arr.length; // exclusive
2. 검사 진행하기
[start, end)로 표기된 범위에서 범위 내 속한 원소 개수는 end - start입니다. 탐색 공간이 남아 있지 않을 때까지 탐색하려면 end - start > 0 인 조건을 만족해야 하는데, 다시 말해 end > start 로 표기할 수 있습니다.
while (end > start) {
// 범위의 중간 검사
}
3. 중간 값 비교하기
int mid = (start + end) / 2;
int value = arr[mid];
중간 값을 구했으면 이 값과 우리가 찾는 값의 대소를 비교하고, 그에 따라 범위를 적절히 조정해 주어야 합니다.
if (value == target) {
return mid;
} else if (value > target) }
// DOWN!
} else {
// UP!
}
value > target은 범위를 작은 쪽으로 좁혀야 합니다. start는 이미 작은 범위에 포함되어 있으므로 변경된 범위의 시작 지점도 start로 유지됩니다. value가 들어 있는 mid에는 target이 들어 있지 않다는 것을 확인했습니다. 따라서 mid - 1까지 포함하는 범위로 좁혀야 합니다.
그리고 value < target은 범위를 큰 족으로 좁혀야 합니다. 이 경우 end가 이미 큰 범위에 포함되어 있으며 mid는 좁혀진 범위에서 제외되어야 합니다.
if (value == target) {
return mid;
} else if (value > target) {
end = mid;
} else {
start = mid + 1;
}
아래는 줄어든 범위를 이용하여 탐색을 반복해 나가면서 계속해서 범위가 줄어들다 정답을 찾으면 해당 인덱스를 반환하고, 정답을 찾지 못하면 반복문 밖에서 -1이 반환되는 binarySearch() 메소드입니다.
private static int binarySearch(int[] arr, int target) {
int start = 0; // inclusive
int end = arr.length; //exclusive
while (end > start) {
int mid = (start + end) / 2;
int value = arr[mid];
if (value == target) {
return mid;
} else if (value > target) {
end = mid;
} else {
start = mid + 1;
}
}
return -1;
}
재귀함수로 구현하는 방법도 있습니다.
/**
* 재귀를 사용하여 이진 알고리즘을 구현합니다.
* @param arr 배열
* @param low 낮은 인덱스
* @param high 높은 인덱스
* @param key 검색할 값
* @return
*/
public static int binarySearch(int[] arr, int low, int high, int key) {
// 1. 높은 인덱스가 낮은 인덱스보다 크거나 같은지 확인합니다.
if (high >= low) {
// 2. 중간 값을 구합니다.
int mid = low + (high - low) / 2;
// 3. 배열의 요소 값이 찾는 값과 동일하면 중간 값을 반환합니다.
if (arr[mid] == key) {
return mid;
}
// 4. 중간 값이 키보다 큰 경우 : 낮은 인덱스와 중간 인덱스에서 1을 뺀 값을 가지고 함수를 재귀적으로 호출합니다.
else if (arr[mid] > key) {
return binarySearch(arr, low, mid - 1, key);
}
// 5. 중간 값이 키보다 작은 경우 : 중간 인덱스에 1을 더하고 높은 인덱스와 함께 함수를 재귀적으로 호출합니다
else {
return binarySearch(arr, mid + 1, high, key);
}
}
// 6. 높은 인덱스가 낮은 인덱스보다 작으면 배열에서 키를 찾지 못했음을 나타내기 위해 -1을 반환합니다.
return -1;
}
자바의 이진 탐색 메서드
| 자료 구조 | 메서드 |
| 배열 | Arrays.binarySearch() |
| 리스트 | Collections.binarySearch() |
자바의 이진 탐색 메서드를 사용할 때 탐색 대상 배열과 리스트는 항상 정렬된 상태여야 한다는 것입니다. 따라서 배열이나 리스트가 정렬되어 있다고 가정할 수 없다면 Arrays.sort()나 Collections.sort() 메서드로 배열이나 리스트를 정렬한 후 이진 탐색을 진행해야 합니다.
int[] array = new int[] {1, 4, 6, 7, 8, 10, 13, 17};
List<Integer> list = List.of(1, 4, 6, 7, 8, 10, 13, 17);
int arrayIndex = Arrays.binarySearch(array, 8);
int listIndex = Collections binarySearch(list, 8);
System.out.println(arrayIndex); // 4
System.out.println(listIndex); // 4
찾고자 하는 값이 없다면 어떤 값을 반환할까요?
int[] array = new int[] {1, 4, 6, 7, 8, 10, 13, 17};
List<Integer> list = List.of(1, 4, 6, 7, 8, 10, 13, 17);
int arrayIndex = Arrays.binarySearch(array, 11);
int listIndex = Collections.binarySearch(array, 11);
System.out.println(arrayIndex); // -7
System.out.println(listIndex); // -7
예제 코드의 반환값인 -7을 양수(7)로 바꾸고, -1을 하면 6이 나옵니다. 이것은 무엇을 뜻할까요?
10의 인덱스가 5고, 13의 인덱스가 6인데, 11이 위 배열에 들어간다면 여섯 번째 인덱스를 차지해야 합니다.
하지만, 코딩 테스트에서는 배열이나 리스트로 탐색 공간을 표현할 수 없는 경우처럼 내장 이진 탐색 메서드를 적용할 수 없을 때가 많이 있습니다. 따라서 직접 이진 탐색을 구현하는 방법을 반드시 익혀 두어야 합니다.